How Attentive are Graph Attention Networks

paper地址 (ICLR2022)

How Attentive are Graph Attention Networks? openreview

Abstract

GAT：

• 在GAT中，每个节点关注它的邻居，并将自己的representation作为query。

• limitation:

  在本文中，我们证明了GAT计算的是一种非常有限的attention: attention scores的排序在query node上是无条件的。（即，注意力分数的排序不因query node而异）

  • 将上述的这种有限的注意力定义为静态注意力（static attention)，并将其与表示更丰富的动态注意力相区分。

  • 由于GAT使用的是静态注意力，因此存在一些他不能表达的简单图问题：

    在一个受控的问题中，我们表明静态注意力甚至阻碍GAT与训练数据拟合。（见4.1节）

提出GATv2：

• 为了解决上述局限性，我们通过修改操作顺序，引入了一个简单的修复办法，并提出了GATv2：一种严格来说比GAT更富表达力的变体。
• 进行了广泛的评估，并表明GATv2在12个OGB和其他基准测试上优于GAT，同时我们匹配了它们的参数成本。
• 代码：https://github.com/tech-srl/how_attentive_are_gats；GATv2作为PyTorch Geometric library，the Deep Graph Library and the TensorFlow GNN library的一部分可用。

1. Introduction

• Velickovi ˇ c et al. (2018) 提出GAT。

在GAT中，每个节点用它自己的表示作为query来关注/处理（attend to)其邻居以更新自己的表示。

这泛化了标准的平均或最大池化邻居（Kipf和Welling，2017; Hamilton等，2017）→ 通过允许每个节点计算其邻居的加权平均值，并（softly）选择其最相关的邻居。

Velickovi ˇ c et al.也将transformer的自注意力机制从序列泛化到图。

• GAT执行一种静态注意力

  对于任何查询节点，注意函数相对于邻居（key）分数是单调的。也就是说，注意系数的排序（目标排序）在图中的所有节点上共享，并且在查询节点上不受影响（即不因查询节点而异）。

  该事实损伤了GAT的表现力。

静态注意力

静态注意力：对于任何 query nodes，注意函数相对于邻域（key）分数是单调的。即：注意系数的排序在图中的所有节点上共享，并且在查询节点上不受条件的影响。如 Figure1 所示：

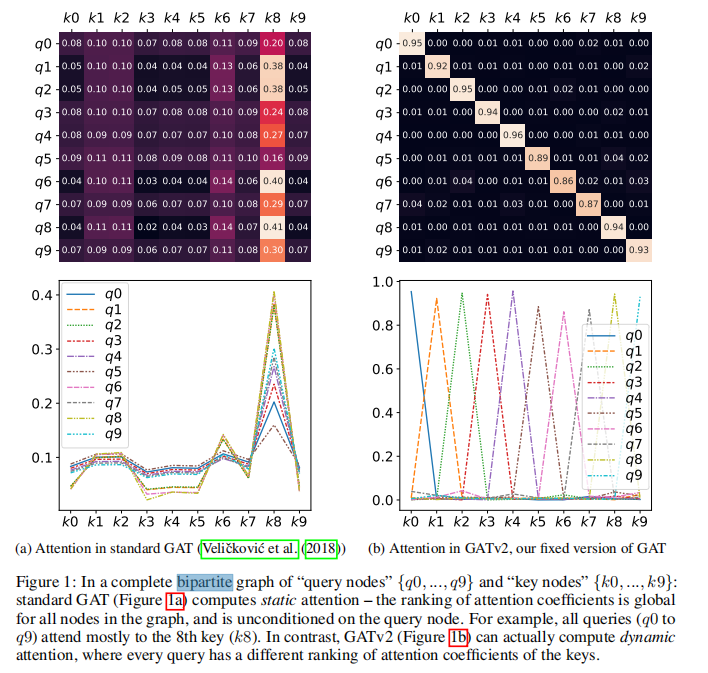
由上面图可以看出，第一幅图就是静态注意力，第二幅图是动态注意力。

第一幅图中每个查询节点q对【k0,k1…k9】计算注意力系数时，都是k8的注意力分数最大，也就是无论q是什么，k8的贡献都是相对最大的。为了解决这个问题，作者提出了GATv2来使用动态注意力，如第二幅图，每个query有对于所有key不同的attention系数的排序

2. PRELIMINARIES

• GNN

  $$h'_i = f_θ (h_i, AGGREGATE ({h_j | j ∈ N_i}))$$

• GAT

  A scoring function e 对于每一个边 （j,i) 计算socre，表示邻居j的特征对节点i的重要性：

  $$e (h_i, h_j ) = LeakyReLU(a^T · [W h_i||W h_j ]) \quad\quad(2)$$

  $a ∈ R^{2d’} , W ∈ R^{d’×d}$，为可学习参数。||表示concatenation。这些注意力分数在所有邻居$j\in N_i$之间使用softmax normalized，定义得到注意力函数为：

  $$α_{ij} = softmax_j (e (h_i, h_j )) = \frac{exp (e (h_i, h_j )) }{\sum _{j'∈N_i}exp (e (h_i, h_j' ))}\quad\quad (3)$$

  然后，GAT使用归一化注意系数计算相邻节点的转换特征（接着用一个非线性σ）的加权平均值，作为i的新表示：

  $$h_i' = σ (\sum _{j∈N_i} α_{ij} · W h_j) \quad\quad (4)$$

3. THE EXPRESSIVE POWER OF GRAPH ATTENTION MECHANISMS

3.1 THE IMPORTANCE OF DYNAMIC WEIGHTING

回答Q：为什么不是动态会限制attention呢？

• Attention

  Attention: Attention是一种机制，它给定一个额外的查询向量（query vector)来计算一组输入key向量的分布。

  如果attention函数总是将一个key的权重计算的至少与其他任何key一样大，而与query无关，那么我们称他为static attention（即不管query是什么，计算的一组key里面，最大的（不小于其他key) 那个是定死的）

• Definition 3.1 （static attention)

  A (possibly infinite) family of scoring functions F ⊆ (Rd × Rd → R) computes static scoring for a given set of key vectors $K=\{k_1, ...,k_n\} ⊂R^d$ and query vectors $Q =\{q_1, ..., q_m\} ⊂R^d$, if for every $f \in F$ there exists a “highest scoring” key $j_f∈ [n]$ such that for every query i∈[m] and key j∈ [n] it holds that $f(q_i,k_{j_f})\ge f(q_i,k_j)$. We say that a family of attention functions computes static attention given K and Q , if its scoring function computes static scoring, possibly followed by monotonic normalization such as softmax.

• 静态注意力非常有限

  静态注意非常有限，因为无论查询如何，每个函数$f\in F$都有一个总是选中的key。这些函数不能模拟不同key对不同query有不同关联的情况。

• Defifinition 3.2 (Dynamic attention)

  A (possibly infifinite) family of scoring functions F ⊆ (Rd × Rd → R) computes dynamic attention for a given set of key vectors $K=\{k_1, ...,k_n\} ⊂R^d$ and $Q =\{q_1, ..., q_m\} ⊂R^d$, if for any mapping $\phi: [m] → [n]$ , there exists $f \in F$ such that for any query $i\in [m]$ and any key $j _{\neq \phi(i)} \in [n]$: $f(q_i, k_ϕ(i)) > f(q_i, k_j)$. We say that a family of attention functions computes dynamic attention for K and Q, if its scoring function computes dynamic scoring, possibly followed by monotonic normalization such as softmax.

  也就是说，动态注意可以通过查询i选择每个键ϕ(i)，使$f(q_i, k_ϕ(i))$在$\{f（q_i，k_j）| j∈[n])\}$中最大。请注意，动态注意和静态注意都是排他性的属性，但它们并不是互补的。此外，每个动态注意族对于相同的K和Q都有严格的静态注意族子集。

• Attending by decaying

  另一种思考注意力的方式是“focus”于最相关的输入的能力。Focusing只能通过衰减其他输入，即，给出这些输入衰减的输入值的分数低于其他输入值。如果一个键的注意力得分总是比其他键相同或更高（如静态注意），那么任何查询都不能忽略这个键或衰减这个键的score.

3.2 THE LIMITED EXPRESSIVITY OF GAT

Theorem 1. A GAT layer computes only static attention, for any set of node representations $K = Q = {h_1, …, h_n}$. In particular, for n > 1, a GAT layer does not compute dynamic attention.

证明：

定理1的结果是，对于任何一组节点V和训练的GAT层，注意函数α定义了一个节点的constant ranking（argsort），无论查询节点i是哪个。即，存在$s_j = a_2^T W h_j$, 我们可以对于任意选择的$h_i$, 得到α相对于每个节点的分数${sj | j∈V}$是单调的。这种全局排序引出了每个邻居群Ni的局部排序。 hi的唯一影响是在所产生的注意力分布的“锐度”上。这在图1a（底部）中得到了演示，其中不同的曲线表示不同的查询（hi）。

Generalization to multi-head attention

对于多头注意力机制，theorem1同样适用于每一个头，得到的输出是静态注意力头的拼接。

3.3 BUILDING DYNAMIC GRAPH ATTENTION NETWORKS

standard GAT 评分函数（Eq.2）的主要问题是学习到的W和a是连续应用的，因此可以分解成一个单一的线性层。为了解决这个限制，我们简单地在非线性(LeakyReLU)之后应用a layer，在拼接之后应用W layer，有效地应用一个MLP来计算每个query-key对的分数：

$$GAT: \quad e (h_i, h_j ) = LeakyReLU(a^T · [W h_i||W h_j ]) \quad (6)$$ $$GATv2 (our\ fixed\ version):\quad e (h_i, h_j ) = a^T LeakyReLU( W · [ h_i||h_j ]) \quad (7)$$

简单的修改对注意功能的表达性有显著的影响：

Theorem 2. A GATv2 layer computes dynamic attention for any set of node representations $K = Q = {h_1, …, h_n}$.

证明见附录A。主要思想是我们可以定义一个适当的函数，GATv2将是一个通用近似器（Cybenko，1989；Hornik，1991）。相比之下，GAT（式（52）)不能近似任何这样的期望的函数（定理1）。

Complexity

• 时间复杂度

both: $O (|V|dd’ + |E|d’)$，可以通过合并线性层减少。

• 参数复杂度：

4. EVALUATION

首先，我们使用一个简单的合成问题（synthetic problem）来证明GAT的弱点，即GAT甚至不能拟合（甚至不能达到较高的训练精度），但很容易通过GATv2来解决（第4.1节）。

第二，我们证明GATv2对边缘噪声更鲁棒，因为它的动态注意机制允许它衰减噪声（假）边缘，而GAT的性能随着噪声的增加而严重降低(第4.2节)。

最后，我们在12个基准测试中比较了GAT和GATv2。（第4.3至4.6节和附录D.3)。我们发现在所有测试GAT的基准测试中都不如GATv2。

4.1 SYNTHETIC BENCHMARK: DICTIONARYLOOKUP

条形码预测问题

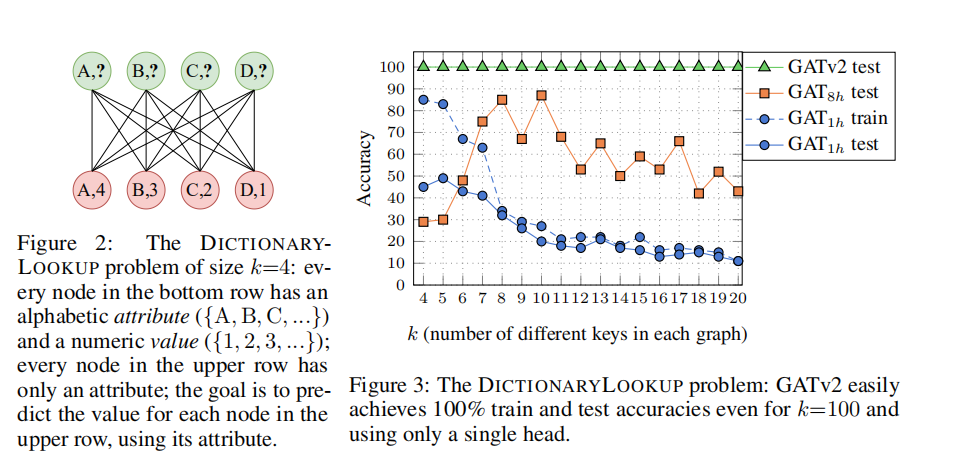
虽然这是一个人为的问题，但它与具有共享多个查询的键的任何子图相关，并且每个查询都需要以不同的方式处理这些键。这样的子图在现实世界的各种领域很常见。

Result

如上右图

• GAT with a single head (GAT1h) failed to fit the training set for any value of k, no matter for how many iterations it was trained, and after trying various training methods.

• GAT8h successfully fits the training set, but generalizes poorly to the test set.

• GATv2 easily achieves 100% training and 100% test accuracies for any value of k, and even for k=100 (not shown) and using a single head

• GIN（non-attentive baselines ）的实验

  

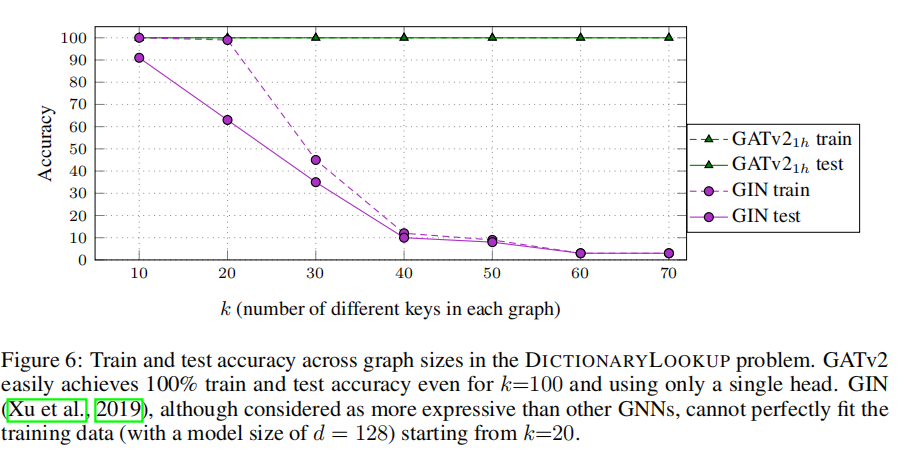
Visualization

见Figure1

The role of multi-head attention

GAT作者发现多头注意的作用是“稳定学习过程”。然而，图3显示，增加头部的数量严格提高了训练的准确性，因此，提高表达性。因此，GAT依赖于有多个注意力头。相比之下，即使是一个GATv2头也比一个多头GAT泛化更好。

Q： 多头注意力缺乏解释性，真的能一定提高准确性吗

A：在实际训练中，有的时候反而下降了呢。为什么呢 （见4.4 NODE-PREDICTION）

4.2 ROBUSTNESS TO NOISE

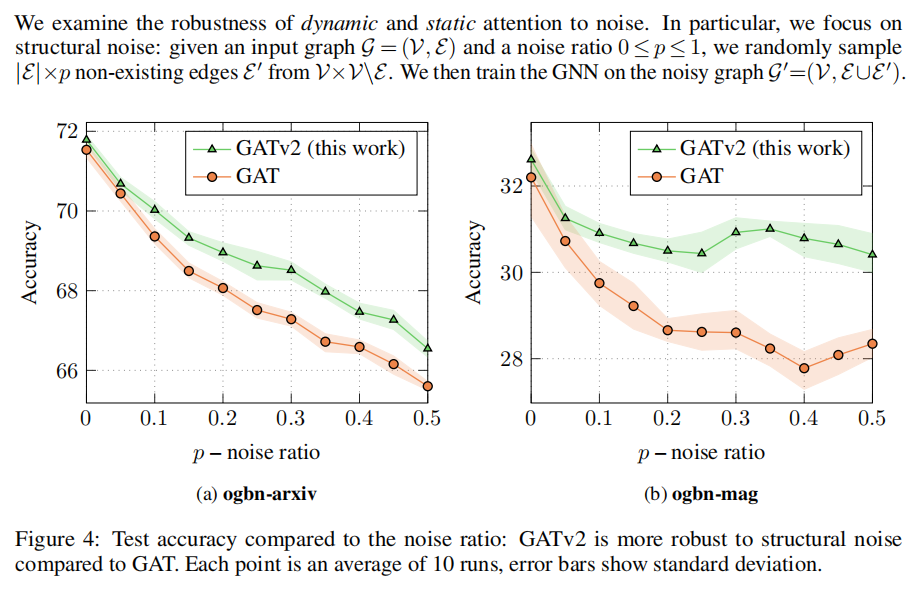
GATv2相比GAT对于噪声受到的影响更小。我们推断动态注意力帮助模型区分噪声边。

4.3 PROGRAMS: VARMISUSE

在Varmisuse的结果

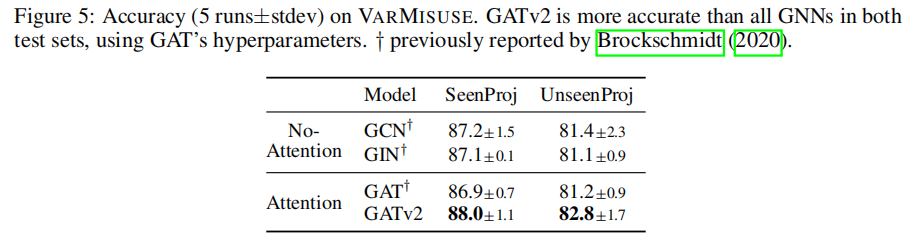
4.4 NODE-PREDICTION

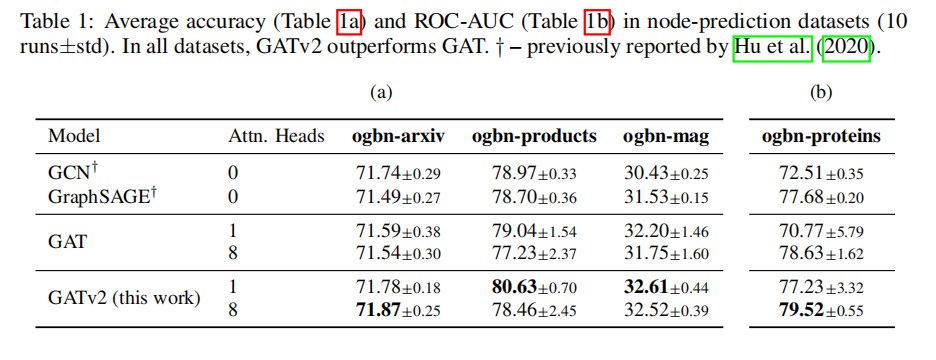
table (a)中，GATv2 一个头的都比GAT多头的要好。

但是，不管是GAT还是GATv2，都可以在表中观察到8头反而没有1头好的情况！四个数据集中，GATv2有两个，GAT有三个。所以？？？

4.5 GRAPH-PREDICTION: QM9

QM9 每个图都是一个分子，其目标是将每个图回归到13个实值的量子化学性质（property)。

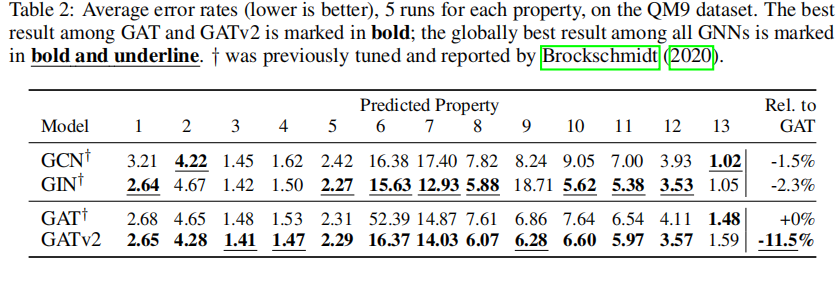
• GATv2比GAT有更低的误差，且比这三个模型都更低误差。

• 存在一些情况是GCN与GIN这类没有应用注意力机制的模型反而表现的更好，我们假设在modeling these properties时不需要注意力。

• 疑问

  1. 观察到一个数据集GAT优于GATv2，说明不是所有情况都一定GATv2优于GAT。首先模型参数他是将GAT调到最优然后直接用于GATv2，不排除GATv2没有调好参数的情况，但是也可能存在一种情况：在某些建模属性/图结构下（比较简单？）并不需要动态注意力呢，或者说动态注意力反而使他更差？→ Discussion部分

  2. 非注意力机制模型GCN等在有些时候反而表现的更好。论文解释是推断可能在modeling these properties时不需要注意力。对于这种情况是否有详细的情况解释呢？

     一个解释例子：当每个邻居的attention都几乎一样的时候，用attention机制基本就没有提升，而多出来的参数会导致优化和训练更难。

4.6 LINK-PREDICTION

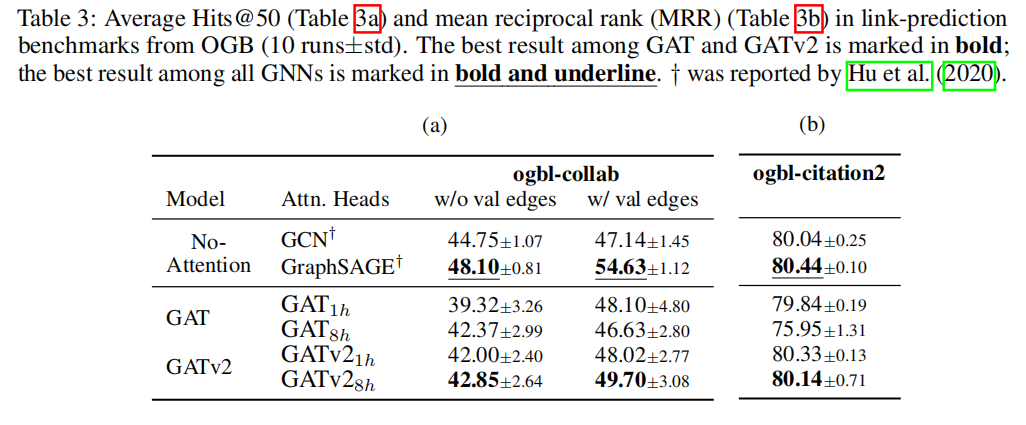
GATv2表现优于GAT。

关于GraphSAGE的表现更好，作者的猜测与假设：

• 我们假设在这些数据集中可能不需要注意。

  

• 另一种可能性是，动态注意力在具有高节点度的图中特别有用：

  在ogbn products和ogbn-proteins中（table1)的平均节点度分别为50.5和597（见附录C中的表5）。然而，ogbl-collab and ogbl-citation2（table 3）的平均节点度要低得多，为8.2和20.7。

• 我们假设，当邻居总数较高时，动态注意机制对于选择最相关的邻居特别有用

提出future work：关于数据集平均节点度的影响这一课题的GNN架构优化

4.7 Discussion

• Which graph attention mechanism should I use?

1. 太简单的任务使用较强的模型可能会过拟合，更强的图注意力机制在节点之间相互越复杂的情况下理论上表现更好。

通常不可能预先确定哪种体系结构的性能最好。一个理论上较弱的模型可能在实践中表现得更好，因为如果任务是“太简单”的且不需要这样的表达能力，一个较强的模型可能会过拟合训练数据。直观地说，我们认为节点之间的相互作用越复杂，GNN从理论上更强的图注意机制中获得的好处就越大，如GATv2。

1. GAT vs GATv2 | 全局排序 vs 邻居排序

主要的问题是，这个problem是否有一个“有影响力的”节点的全局排名（GAT就足够了），或者不同的节点是否有不同邻居的邻居排名（使用GATv2）。

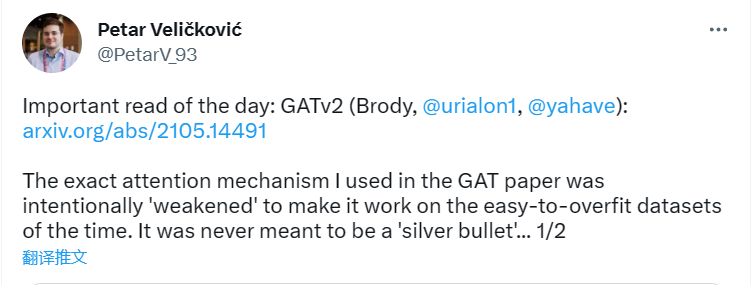
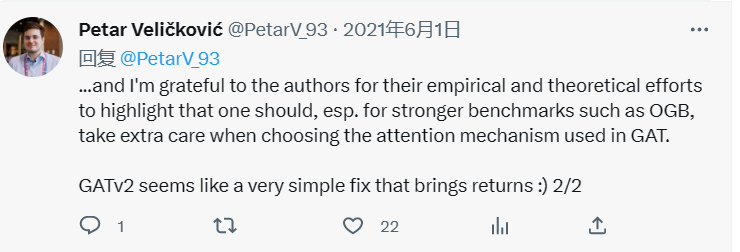
GAT的作者在推特上证实，GAT的设计适用于当时（2017年）“容易过拟合”的的数据集，如Cora、Citeseer（Senetal.，2008年），他们这些数据集可能具有“globally important”节点的底层静态排名。GAT的作者同意这一观点：更新和更具挑战性的基准测试可能需要更强的注意机制，如GATv2。在本文中，我们回顾了传统的假设，并表明许多现代图基准和数据集包含更复杂的交互，因此需要动态的注意力。

5. Conclusion

在本文中，我们发现流行和广泛使用的图注意网络不计算动态注意。相反，在标准定义和实现中的注意机制的结果只是静态的：对于任何查询，它的邻居分数对于每个节点的分数是单调的。因此，GAT甚至不能表达简单的对齐问题。为了解决这个限制，我们引入了一个简单的修复并提出了GATv2：通过修改GAT中的操作顺序，GATv2实现了一个通用的近似注意函数，因此严格比GAT更强大。

我们在一个需要动态选择节点的综合问题中，展示了GATv2相对于GAT的经验优势，以及来自OGB和其他公共数据集的11个基准测试。我们的实验表明GATv2在所有基准测试中都优于GAT，同时具有相同的参数代价。

我们鼓励社区在将新的GNN架构与常见的强基线进行比较时，使用GATv2而不是GAT。在复杂的任务和领域中，以及在具有挑战性的数据集中，一个模型使用GAT作为内部组件可以用GATv2替换它，以适应严格上更强大的模型。为此，我们在https://github.com/tech-srl/how_attentive_are_gats 上公开了我们的代码，并且GATv2可以作为PyTorch Geometric library, the Deep Graph Library, and TensorFlow GNN的一部分使用。在 https://nn.labml.ai/graphs/gatv2 上有一个带注释的实现 。