图基本知识

Posted on Edited on In Views: Waline: Word count in article: 4.3k Reading time ≈ 4 mins.

图基本知识

图的表示

点和边构成的数据结构

日常生活中无处不在：图像：像素和像素之间的连接构成的图; 网页： 网页之间的跳转;

分类

无向图和有向图

表示

  • 邻接矩阵

图的性质

度

  • 无向图的度==该节点连接的边的数量
  • 有向图的度
    • 出度：从该节点指向的边的数量
    • 入度：指向该节点的边的数量

子图

​ 子图所有的节点都包含在大图里面；

​ 子图的边都是大图的边的子集；

连通图和连通分量

无向图

  • 连通图：

    任意节点i能够通过一些边到达节点j，则称之为连通图；反之非连通图。

    对于一个无向图：没有孤立的节点其实都能连通

  • 连通分量：
    无向图G的一个极大连通子图称为G的一个连通分量（或连通分支）。

    连通图只有一个连通分量：他本身；非连通图有多个连通分量。

有向图的连通性

  • 强连通图：给定图G的任意两个结点u,v可互相到达。
  • 弱连通图：至少有一对结点不满足单向连通，但去掉边的方向之后从无向图的观点看是连通图。

最短路径和图直径

两结点的最短到达路径就是最短路径

两两结点的最短路径中的长度最大值是图直径。

度中心性

$N_{degree}$表示该节点的度，n为该节点所在图的节点总数。

特征向量中心性Eigenvector Centrality

最大特征值对应的特征向量作为特征向量中心性的对比指标。

A为邻接矩阵；

如图，最大的特征值是第一个，所以特征向量对应第一列。

（特征向量中心性将特征向量的负值变成正进行统一对比）

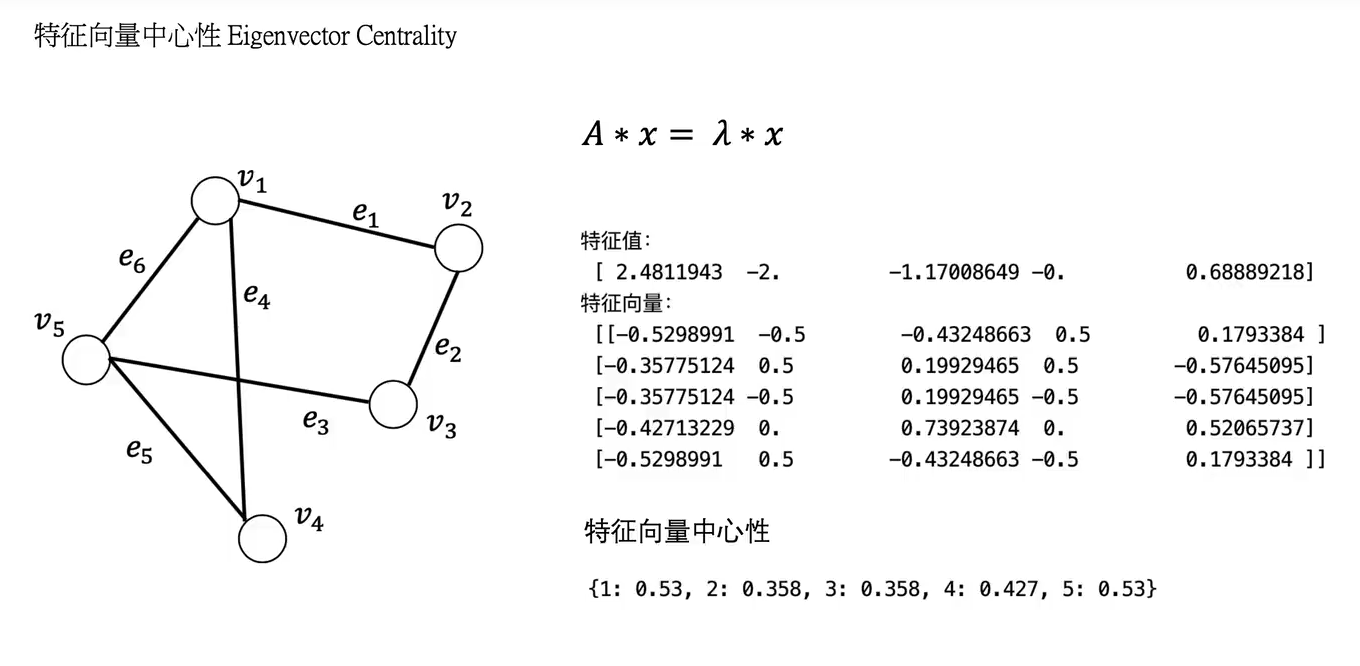
特征向量中心性不仅考虑了自己节点的度，还考虑了和他向量节点的度的情况。如v4的值会比v2和v3大是因为它虽然度和v2\v3一样大，但是相连的是v1和v5，比v2/v3向量的节点的度总体要大。

conclu:特征向量中心性比度中心性可以更好的表示节点在图中所处的位置。

中介中心性 Betweenness Centrality

连接中心性 Closeness

​ n为节点总数；

网页排序算法

pagerank

边的pagerank值为节点向外指向时平分的结果。如节点2向外指向的边有两条，因此现在那两条边的pagerank值都为pagerank2/2。

节点的pagerank值即为指向它的边的值的和。

不断的迭代，最后每个节点的pagerank值达到稳态 。

阻尼系数：如节点3到节点4的概率有0.15。

HITS

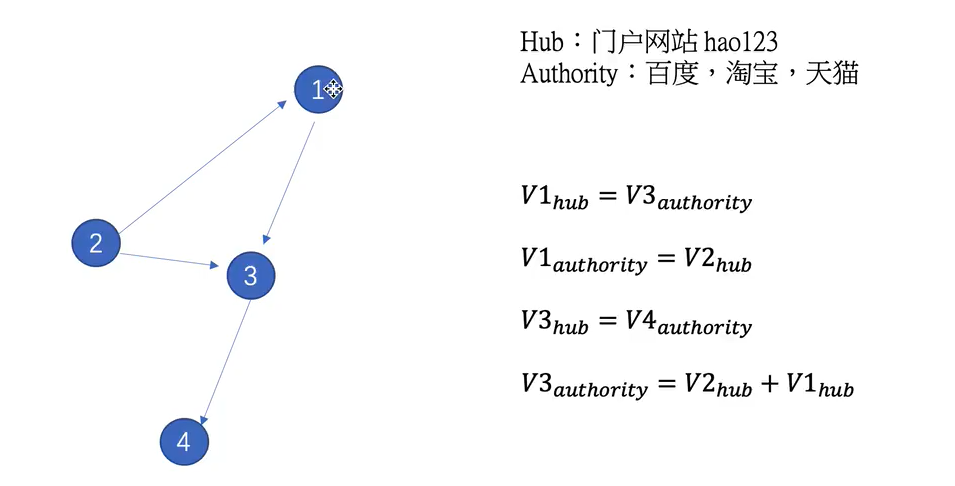
每个节点都有authority值和hub值

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import numpy as np
import pandas as pd
import networkx as nx
import random

lis =lambda x:random.randint(1,6)

edges  = pd.DataFrame()
edges['sources'] = [lis(x) for x in range(12)]
edges['targets'] = [lis(x) for x in range(12)]
edges['weights'] = [1 for x in range(12)]

G = nx.from_pandas_edgelist(edges,source='sources',target='targets',edge_attr='weights')
print("G:",G)
print(nx.__version__)
print(nx.adjacency_matrix(G))
#度
print("degree:",nx.degree(G))
# 连通分量
print("connected_components",list(nx.connected_components(G)))
#图直径
print("diameter:",nx.diameter(G))
# 度中心性
print("degree_centrality:",nx.degree_centrality(G))
#特征向量中心性
print("eigenvector:",nx.eigenvector_centrality(G))
# betweenness 中介中心性
print("betweenness:",nx.betweenness_centrality(G))
# closeness 连接中心性
print("closenesss:",nx.closeness_centrality(G))
#pagerank
print("pagerank:",nx.pagerank(G))
#hits
print("hits:",nx.hits(G))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
FutureWarning: adjacency_matrix will return a scipy.sparse array instead of a matrix in Networkx 3.0.
  print(nx.adjacency_matrix(G))
G: Graph with 6 nodes and 8 edges
2.8.4
  (0, 0)	1
  (0, 2)	1
  (0, 3)	1
  (0, 4)	1
  (1, 1)	1
  (1, 4)	1
  (1, 5)	1
  (2, 0)	1
  (2, 3)	1
  (3, 0)	1
  (3, 2)	1
  (4, 0)	1
  (4, 1)	1
  (5, 1)	1
degree: [(3, 5), (1, 4), (4, 2), (2, 2), (5, 2), (6, 1)]
connected_components [{1, 2, 3, 4, 5, 6}]
diameter: 4
degree_centrality: {3: 1.0, 1: 0.8, 4: 0.4, 2: 0.4, 5: 0.4, 6: 0.2}
eigenvector: {3: 0.6845438993664699, 1: 0.2664667519552274, 4: 0.4038050904760662, 2: 0.4038050904760662, 5: 0.3528502881437044, 6: 0.09886704157967073}
betweenness: {3: 0.6000000000000001, 1: 0.4, 4: 0.0, 2: 0.0, 5: 0.6000000000000001, 6: 0.0}
closenesss: {3: 0.625, 1: 0.5, 4: 0.45454545454545453, 2: 0.45454545454545453, 5: 0.625, 6: 0.35714285714285715}
pagerank: {3: 0.26059842893288254, 1: 0.22624644367910318, 4: 0.1397855189975688, 2: 0.1397855189975688, 5: 0.1444805278346477, 6: 0.08910356155822868}
hits: ({3: 0.3097026575730737, 1: 0.1205522404859372, 4: 0.18269069072963665, 2: 0.18269069072963665, 5: 0.1596357156065535, 6: 0.04472800487516233}, {3: 0.30970265757307375, 1: 0.1205522404859372, 4: 0.1826906907296366, 2: 0.18269069072963656, 5: 0.1596357156065534, 6: 0.04472800487516234})

视频来源：https://www.bilibili.com/video/BV1aB4y1Q7RL

Graph Embedding

代码

  1. DeepWalk :采用随机游走，形成序列，采用skip-gram方 式生成节点embedding。
  2. node2vec :不同的随机游走策略，形成序列，类似skip-gram方 式生成节点embedding。
  3. LINE :捕获节点的一-阶和二阶相似度，分别求解，再将一阶二阶拼接在一起， 作为节点的embedding
  4. struc2vec :对图的结构信息进行捕获，在其结构重要性大于邻居重要性时，有较好的效果。
  5. SDNE :采用了多个非线性层的方式捕获一阶二阶的相似性。

DeepWalk

  • 适用于无向图

随机游走获得节点序列

使用skipgram算法完成嵌入

window size d是向前向后看多少个节点

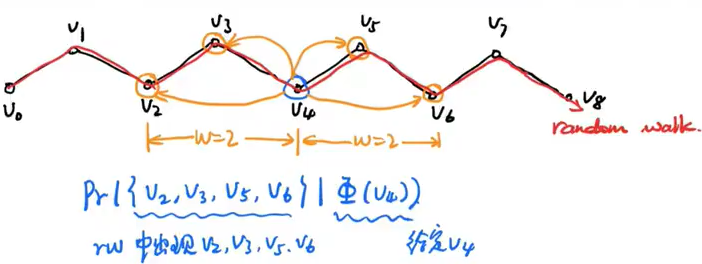
算法：

如下图：给定v4节点，算出v2,v3,v5,v6同时出现的概率。然后完成嵌入。

  • embedding效果对比，看参数作用

    DeepWalk是无监督的完成图嵌入，效果判别通过将完成嵌入的图（有label)输入分类器,看分类效果

    • embedding size d

      d变大，效果

      一定范围内上升，超过一定值，反而下降

    • 迭代次数

​ 迭代次数增加，效果上升；到达一定值再增加，效果变化有限

LINE

large-scale Information Network Embedding

作者提出LINE用于大规模图上表示节点之间的结构信息表现比较好

  • 一阶：局部的结构信息。
  • 二阶：节点的邻居。共享邻居的节点可能是相似的。

一阶相似性：两个节点相连接，且边的权重很大，那么他们的一阶相似性很高

二阶相似性： 两个节点的邻居很相似，那么即使这两个节点没有相互连接，他们的二阶相似性也很大

如图，六节点和七节点一阶相似性高，五节点和六节点的embedding的二阶相似性很高：

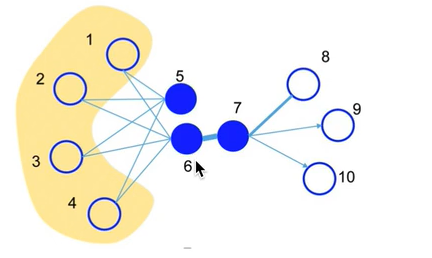
  • 节点的度比较低的话，使用LINE效果不会很好

  • 适用于有向图和无向图

一阶和二阶embedding训练的loss：

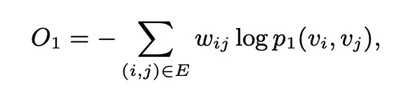
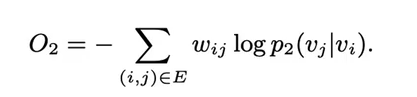
最后的embedding是一阶和二阶的直接拼接

Node2Vec

和DeepWalk相似，不同的是采用了有策略的游走

游走策略：

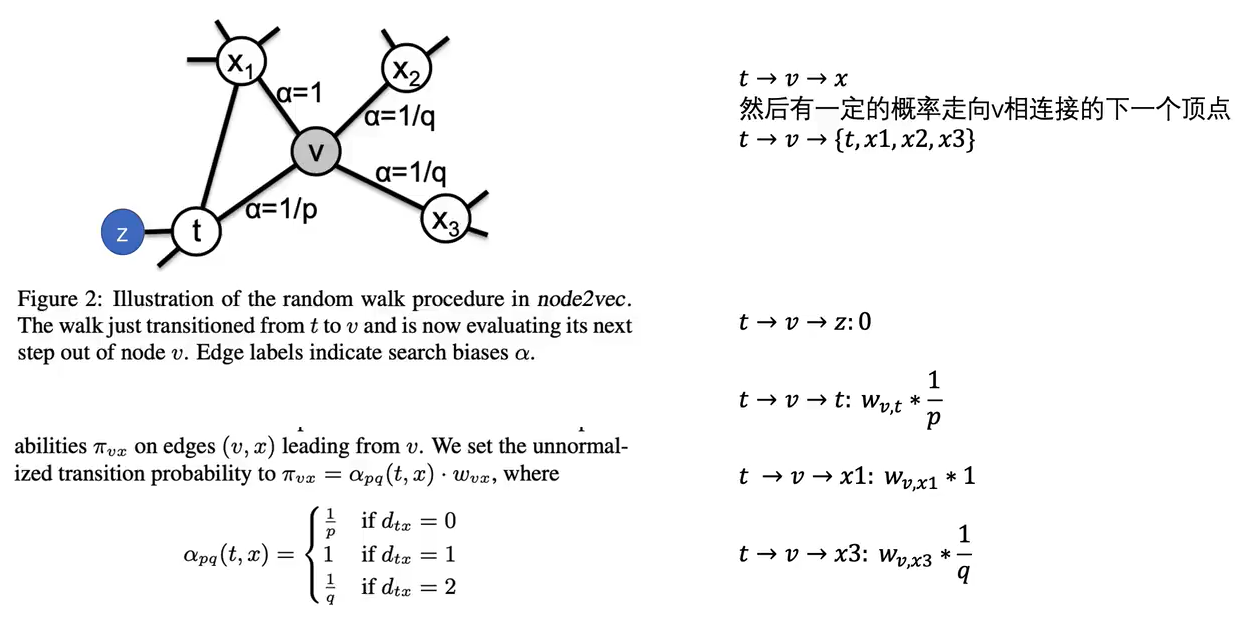
DFS，即q值小，探索性强，会捕捉同质性节点，即相邻节点表示类似；BFS，即p值小，保守周围，会捕捉结构性，即某些节点的图上结构类似。

struct2vec

之前的方式都是基于近邻，但是有些节点没有近邻也有结构相似性

SDNE

structural deep network embedding

涉及 autoencoder的思想